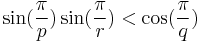Schläfli–Hess polychoron

In four-dimensional geometry, Schläfli–Hess polychora are the complete set of 10 regular self-intersecting star polychora (four-dimensional polytopes). They are named in honor of their discoverers: Ludwig Schläfli and Edmund Hess. Each is represented by a Schläfli symbol {p,q,r} in which one of the numbers is 5/2. They are thus analogous to the regular nonconvex Kepler–Poinsot polyhedra.

Allowing for regular star polygons as cells and vertex figures, these 10 polychora add to the set of six regular convex 4-polytopes. All may be derived as stellations of the 120-cell {5,3,3} or the 600-cell {3,3,5}.

Contents

History

Four of them were found by Ludwig Schläfli while the other six were skipped because he would not allow forms that failed the Euler characteristic on cells or vertex figures (for zero-hole tori: F − E + V = 2). That excludes cells and vertex figures as {5,5/2}, and {5/2,5}.

Edmund Hess (1843–1903) published the complete list in his 1883 German book Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder.

Names

Their names given here were given by John Conway, extending Cayley's names for the Kepler–Poinsot polyhedra: along with stellated and great, he adds a grand modifier. Conway offered these operational definitions:

  1. stellation – replaces edges by longer edges in same lines. (Example: a pentagon stellates into a pentagram)
  2. greatening – replaces the faces by large ones in same planes. (Example: an icosahedron greatens into a great icosahedron)
  3. aggrandizement – replaces the cells by large ones in same 3-spaces.

Symmetry

All ten polychora have [3,3,5] (H4) hexacosichoric symmetry. They are generated from 6 related rational-order symmetry groups: [3,5,5/2], [5,5/2,5], [5,3,5/2], [5/2,5,5/2], [5,5/2,3], [3,3,5/2].

Each group has 2 regular star-polychora, except for two groups which are self-dual, having only one. So there are 4 dual-pairs and 2 self-dual forms among the ten regular star polychora.

Table of elements

Note:

The cells (polyhedra), their faces (polygons), the polygonal edge figures and polyhedral vertex figures are identified by their Schläfli symbols.

Name
 Wireframe Solid Schläfli
{p, q,r}
Coxeter–Dynkin		 Cells
{p, q}		 Faces
{p}		 Edges
{r}		 Vertices
{q, r}		 Density χ Dual
{r, q,p}
Icosahedral 120-cell {3,5,5/2}
 120
{3,5}
 1200
{3}
 720
{5/2}
 120
{5,5/2}
 4 480 Small stellated 120-cell
Small stellated 120-cell {5/2,5,3}
 120
{5/2,5}
 720
{5/2}
 1200
{3}
 120
{5,3}
 4 −480 Icosahedral 120-cell
Great 120-cell {5,5/2,5}
 120
{5,5/2}
 720
{5}
 720
{5}
 120
{5/2,5}
 6 0 Self-dual
Grand 120-cell {5,3,5/2}
 120
{5,3}
 720
{5}
 720
{5/2}
 120
{3,5/2}
 20 0 Great stellated 120-cell
Great stellated 120-cell {5/2,3,5}
 120
{5/2,3}
 720
{5/2}
 720
{5}
 120
{3,5}
 20 0 Grand 120-cell
Grand stellated 120-cell {5/2,5,5/2}
 120
{5/2,5}
 720
{5/2}
 720
{5/2}
 120
{5,5/2}
 66 0 Self-dual
Great grand 120-cell {5,5/2,3}
 120
{5,5/2}
 720
{5}
 1200
{3}
 120
{5/2,3}
 76 −480 Great icosahedral 120-cell
Great icosahedral 120-cell {3,5/2,5}
 120
{3,5/2}
 1200
{3}
 720
{5}
 120
{5/2,5}
 76 480 Great grand 120-cell
Grand 600-cell {3,3,5/2}
 600
{3,3}
 1200
{3}
 720
{5/2}
 120
{3,5/2}
 191 0 Great grand stellated 120-cell
Great grand stellated 120-cell {5/2,3,3}
 120
{5/2,3}
 720
{5/2}
 1200
{3}
 600
{3,3}
 191 0 Grand 600-cell

Existence

The existence of a regular polychoron 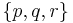\{p,q,r\} is constrained by the existence of the regular polyhedra 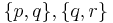\{p,q\}, \{q,r\} and a dihedral angle constraint:

The six regular convex polytopes and 10 star polytopes above are the only solutions to these constraints.

There are four nonconvex Schläfli symbols {p,q,r} that have valid cells {p,q} and vertex figures {q,r}, and pass the dihedral test, but fail to produce finite figures: {3,5/2,3}, {4,3,5/2}, {5/2,3,4}, {5/2,3,5/2}.

See also

References

External links